MOVIMIENTO ARMÓNICO SIMPLE

Comprende el estudio de las ondas a partir del análisis de las vibraciones que se presentan en los diferentes medios, teniendo en cuenta el péndulo simple y las formas más presentes de oscilaciones en otros casos interpretados como movimiento armónico simple (M.A.S). 
es un movimiento vibratorio bajo la acción de una fuerza recuperadora elástica, proporcional al desplazamiento y en ausencia de todo rozamiento. 
Solemos decir que el sonido de una determinada nota musical se representa gráficamente por la función seno. Ésta representa un movimiento vibratorio llamado movimiento armónico simple, que es aquel que se obtiene cuando los desplazamientos del cuerpo vibrante son directamente proporcionales a las fuerzas causantes de este desplazamiento. 
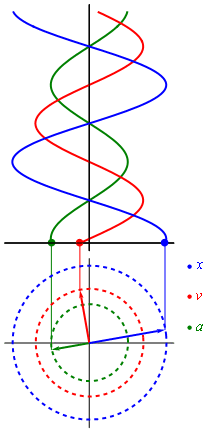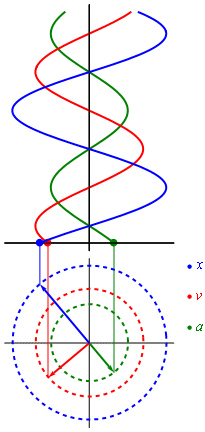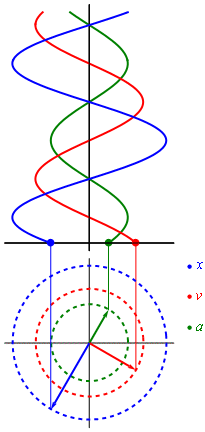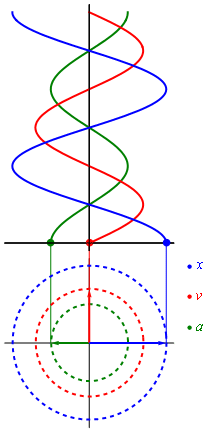
Un ejemplo de este movimiento se puede encontrar a partir del desplazamiento de un punto cualquiera alrededor de toda la longitud de una circunferencia. Cuando un punto (P) recorre una circunferencia con velocidad uniforme, su proyección (Q) sobre cualquiera de los diámetros de esta, realiza un tipo de movimiento armónico simple. Cada vez que el punto se encuentre en uno de los cuatro cuadrantes de la circunferencia, se trazará una perpendicular desde el punto a un diámetro fijo de la circunferencia. A medida que el punto escogido se mueve a velocidad uniforme, el punto proyectado en el diámetro, realizará un movimiento oscilatorio rectilíneo. 

Para representar gráficamente (en una función) el movimiento armónico simple de un punto, se toman como abscisas los tiempos medidos como fracciones del período (T/12, T/6, T/4...) que es el tiempo que este punto tarda en dar una vuelta completa a la circunferencia; y como a ordenadas las sucesivas prolongaciones del mismo. La resultante es una sinusoide, ya que la variación del tiempo t, se traduce como una variación delsin x, donde x es el ángulo que forma el radio con el semi-eje positivo de abscisas (x es proporcional al tiempo).

ECUACIONES DE MOVIMIENTO ARMÓNICO SIMPLE.

Interpretación simbólica y relación matemática extraída del análisis de los fenómenos físicos del movimiento oscilatorio que representa su comportamiento, en forma de ecuaciones características de algunas situaciones particulares que se estudian de acuerdo a los parámetros conocidos sobre el movimiento.

La posición de una partícula que sigue un movimiento armónico simple ( m.a.s.), también denominada elongación, viene determinada por la distancia x a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m). Se trata de una función sinusoidal (seno o coseno), que depende del tiempo x = f(t).

Ecuación de posición

	x → Seno	x → Coseno
Conω	x=A⋅sin(ω⋅t+φ0)	x=A⋅cos(ω⋅t+φ'0)
Conf	x=A⋅sin(2⋅π⋅f⋅t+φ0)	x=A⋅cos(2⋅π⋅f⋅t+φ'0)
ConT	x=A⋅sin(2⋅πT⋅t+φ0)	x=A⋅cos(2⋅πT⋅t+φ'0)

 Donde

·         A: Amplitud máxima del movimiento. Representa la distancia máxima a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)

·         f: Frecuencia del movimiento. Es el número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.

·         T: Periodo del movimiento. El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).

·         ω : Frecuencia angular o pulsación. Representa el número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Se encuentra relacionada con la frecuencia y el periodo del movimiento según ω=2⋅πT=2⋅π⋅f  

·         φ0  y φ'0 : Fase inicial. Se trata del ángulo que representa el estado inicial de vibración, es decir, la posición x del cuerpo en el instante t = 0. Su valor depende de si has elegido un seno o un coseno para representar el movimiento. φ'0=φ0−π/2 Su unidad de medida en el Sistema Internacional es el radián (rad) .

Para cualquier instante t se cumple que x(t)=x(t+T) .

Gráfica de posición x - t

Velocidad

La velocidad instantánea determina la variación de posición que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la posición respecto al tiempo.

v=dxdt

Para obtener la expresión de la velocidad hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno

 MOVIMIENTO DE ONDA.

Caracterización que se le da a los tipos de movimiento en física determinados como movimientos periódicos, movimientos amortiguados, movimientos forzados y movimientos simples.

En física, una onda (del latín unda) consiste en la propagación de una perturbación de alguna propiedad de un medio, por ejemplo, densidad, presión, campo eléctrico o campo magnético, a través de dicho medio, implicando un transporte de energía sin transporte de materia. El medio perturbado puede ser de naturaleza diversa como aire, agua, un trozo de metal e, incluso, inmaterial como el vacío.

El movimiento ondulatorio es la propagación de una onda por un medio material o en el vacío. Sin que exista la transferencia de materia, ya sea por ondas mecánicas o electromagnéticas.

Una onda es una perturbación de alguna propiedad de un medio (densidad, presión, campo electromagnetico,...).

La onda transporta energía. Y así todo tipo de onda se adquiere más fácil ya sea haciendo una ecuación o sustituyendo la respuesta más rápidamente.